[Physics | Car Racing | mechanical advantage | Friction | Machines | Mechanical Engineering] This equation approximates the maximum speed a car could achieve on a banked turn of a selected NASCAR track.
The inputs to this equation are:
- r - the radius of the track's turn
- `phi` - the angle of the banked turn
- `mu` - the coefficient of friction characterizing the tires.
Note that we've set the default value for the frictional coefficient to 1.1. You can still modify the value if you have a better value to plug-in. Many sites calculate frictional coefficients for auto tires and come up with values in the range of 0.7 to 1.0. But information from sources closer to racing suggest that with special rubber and tire construction the true value of the frictional coefficient for racing tires may be as high as 1.3. It is also known that the frictional coefficient goes down throughout the race as tires wear down. Pit crews actually calculate the projected wear to maximize the time at which they will pull-in to put on new tires. Their data comes from historic lap times on the same track and the fact those lap times consistently decrease during every race for every car. The software they use actually does a curve fit to the historic data to identify the decrease in speed due to change in coefficient of friction. Math in action on the NASCAR circuit!
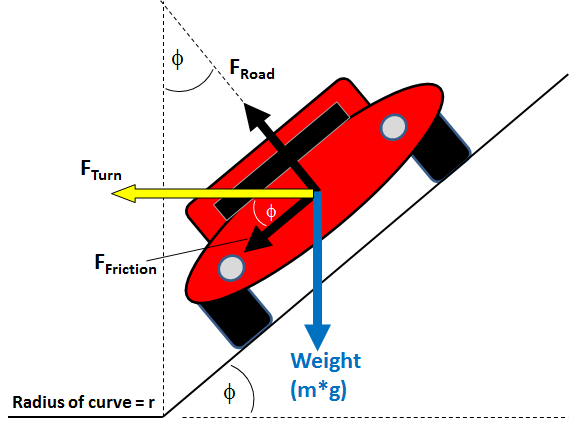
Notes
In the illustration, we see the back end of a car turning to the left. The weight of the car due to the force of gravity pushes downward. That force is equal and opposite to the vertical component of the force of the road pushing up on the car's tires. The frictional force, `F_"Friction"`, is toward the direction of the turn and parallel to the banked surface and keeps the car from sliding outward during the turn.
The force of the road pushing up (perpendicular to the road surface) on the car is is the force `F_"Road"`.
We can determine the maximum velocity, v, by assuming the horizontal forces sum exactly to zero. We first compute the force exerted on the car's tires by the road, `F_"Road"`:
Eq. 1: `sum F_"Vertical" = F_"Road" * cos(phi) - F_"Road" * mu * sin(phi) - m*g = 0`
Thus we can compute `F_"Road" * mu = F_"Friction"` from Eq. 1 as:
Eq. 2: `F_"Road" * (cos(phi) - mu * sin(phi)) = mg`
Eq. 3: `F_"Road" = mg`/`(cos(phi) - mu * sin(phi))`
We then substitute `F_"Road"` into the following equation:
Eq. 4: `sum F_"Horizontal" = F_"Road" * sin(phi) + mu*F_"Road" * cos(phi) = m*v^2/r`
which provides us:
Eq. 5: `((m*g)/ (cos(phi) - mu * sin(phi))) * sin(phi) + ((m*g)/(cos(phi) - mu * sin(phi))) * mu * cos(phi) =m*v^2/r`
Eq. 6: `((r*g) / (cos(phi) - mu * sin(phi))) * (sin(phi) + mu * cos(phi)) = v^2`
Eq. 7: `v = sqrt( (r*g * (sin(phi) + mu * cos(phi))) / (cos(phi) - mu * sin(phi)) )`